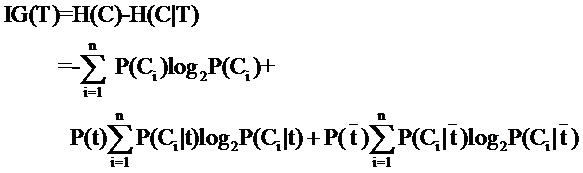python计算信息增益 (information gain)

在文本分类中有这样一个场景，当我们已经分好词，并构造出词频向量后，这个向量会很大，经常会多达几万维，甚至十几万维。这种规模的模型如果要用SVM等较高级的机器学习进行训练的话，那简直是慢的要死，深度学习就再别谈了。为了较少向量维度，我们可以采用一些方法，比如在词向量中过滤掉词频小于N的词，这个N可以自己定，但一般取值比较小。采用这种方法能有效降低向量维度，但是还是不够。我们不能为了降低向量维度到一定的程度而不断地增大N值，因为这种过滤掉低频次的方法，对向量维度的减少是随着N的增大而逐步降低的，比如说：将N=1，你可以过滤掉10000个单词；接着N=2，你过滤掉了15000个单词；N=3，过滤掉16000个单词；N=4，过滤掉了16800个单词。所以这种方法适用于粗糙地降维。我们可以在原始数据集上利用这种方法先过滤一波词。然后再想别的方法。
那么怎样才能将向量的维度降到我们想要的大小，而不会对整个系统的信息产生重大影响呢？这个问题就是特征选择的问题。
特征选择有2个很明显的优点：

减少特征数量、降维，使模型泛化能力更强，减少过拟合
增强对特征和特征值之间的理解一般对于文本分类有两种最常用的信息选择方法。

一个是卡方检验，另一个是信息增益。但凡是特征选择，总是在将特征的重要程度量化之后再进行选择，而如何量化特征的重要性，就成了各种方法间最大的不同。开方检验中使用特征与类别间的关联性来进行这个量化，关联性越强，特征得分越高，该特征越应该被保留。
在信息增益中，重要性的衡量标准就是看特征能够为分类系统带来多少信息，带来的信息越多，该特征越重要。本文只针对信息增益，卡方检验请自行谷歌度娘。关于信息增益，大牛Jasper有一篇十分精彩的博文来进行介绍，其计算方法Jasper已经说得十分清楚了。建议你看完这篇文章，再来继续阅读本文。信息增益最后的推导公式为：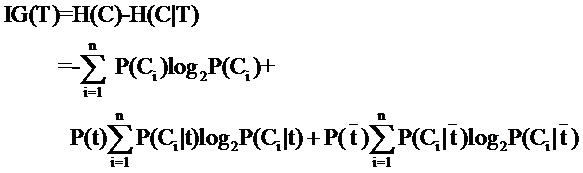
我们现在要用python来实现信息增益的计算。

假设我们有4篇文档，每篇文档都已经分好词了：

文档1： 鲜花 体育
文档2： 太阳 大象 体育
文档3: 大象

假设我们词的索引是：
[鲜花，太阳，大象，体育]
那么我们的文档构造好的词频向量分别是：

文档1：[1,0,0,1]
文档2：[0,1,1,1]
文档3：[0,0,1,0]

假设3篇文档的分类分别是：文档1和文档2属于“0”类，文档3属于“1”类。那么我们程序的输入就是X，y：
X代表词频向量组成的矩阵

[[1,0,0,1], 
 [0,1,1,1],
 [0,0,1,0]]

y代表标签向量
[0,0,1]
我们利用numpy包中的矩阵来包装X，因为它可以提供许多方便的高级函数。下面就贴上代码，代码里有注释，有兴趣的同学可以好好研究一下，如果你想拿来直接用的话，也是没问题的。代码的效率应该还是可以的，其中有一个比较巧妙的矩阵的转秩。可以好好理解一下：

#coding: utf-8
import numpy as np
'''
    计算信息增益
    powerd by ayonel
'''
class InformationGain:
    def __init__(self, X, y):
        self.X = X
        self.y = y
        self.totalSampleCount = X.shape[0]      # 样本总数
        self.totalSystemEntropy = 0             # 系统总熵
        self.totalClassCountDict = {}           # 存储每个类别的样本数量是多少
        self.nonzeroPosition = X.T.nonzero()    # 将X转置之后输出非零值的位置
        self.igResult = []                      # 保存结果的list
        self.wordExistSampleCount = 0
        self.wordExistClassCountDict = {}
        self.iter()


    # 将结果列表排序输出
    def get_result(self):
        return self.igResult

    # 计算系统总熵
    def cal_total_system_entropy(self):
        # 计算每个类别各有多少个
        for label in self.y:
            if label not in self.totalClassCountDict:
                self.totalClassCountDict[label] = 1
            else:
                self.totalClassCountDict[label] += 1
        for cls in self.totalClassCountDict:
            probs = self.totalClassCountDict[cls] / float(self.totalSampleCount)
            self.totalSystemEntropy -= probs * np.log(probs)


    # 遍历nonzeroPosition时，逐步计算出每个word的信息增益
    def iter(self):
        self.cal_total_system_entropy()

        pre = 0
        for i in range(len(self.nonzeroPosition[0])):
            if i != 0 and self.nonzeroPosition[0][i] != pre:
                for notappear in range(pre+1, self.nonzeroPosition[0][i]):  # 如果一个词在整个样本集中都未出现，则直接赋为0
                    self.igResult.append(0.0)
                ig = self.cal_information_gain()
                self.igResult.append(ig)
                self.wordExistSampleCount = 0
                self.wordExistClassCountDict = {}
                pre = self.nonzeroPosition[0][i]
            self.wordExistSampleCount += 1
            yclass = self.y[self.nonzeroPosition[1][i]]  # 求得当前样本的标签
            if yclass not in self.wordExistClassCountDict:
                self.wordExistClassCountDict[yclass] = 1
            else:
                self.wordExistClassCountDict[yclass] += 1
        # 计算最后一个单词的ig
        ig = self.cal_information_gain()
        self.igResult.append(ig)

    # 计算ig的主要函数
    def cal_information_gain(self):
        x_exist_entropy = 0
        x_nonexist_entropy = 0

        for cls in self.wordExistClassCountDict:
            probs = self.wordExistClassCountDict[cls] / float(self.wordExistSampleCount)
            x_exist_entropy -= probs * np.log(probs)

            probs = (self.totalClassCountDict[cls] - self.wordExistClassCountDict[cls]) / float(self.totalSampleCount - self.wordExistSampleCount)
            if probs == 0: #该单词在每条样本中都出现了，虽然该几率很小
                x_nonexist_entropy = 0
            else:
                x_nonexist_entropy -= probs*np.log(probs)

        for cls in self.totalClassCountDict:
            if cls not in self.wordExistClassCountDict:
                probs = self.totalClassCountDict[cls] / float(self.totalSampleCount - self.wordExistSampleCount)
                x_nonexist_entropy -= probs*np.log(probs)

        # 合并两项，计算出ig
        ig = self.totalSystemEntropy - ((self.wordExistSampleCount/float(self.totalSampleCount))*x_exist_entropy +
                                        ((self.totalSampleCount-self.wordExistSampleCount)/float(self.totalSampleCount)*x_nonexist_entropy))
        return ig
if __name__ == '__main__':
    X = np.array([[1,0,0,1],[0,1,1,1],[0,0,1,0]])
    y = [0,0,1]
    ig = InformationGain(X, y)
    print(ig.get_result())

以上程序运行结果： [0.17441604792151594, 0.17441604792151594, 0.17441604792151594, 0.63651416829481278]
上面的结果代表着鲜花的信息增益：0.17441604792151594 太阳的信息增益：0.17441604792151594 大象的信息增益：0.17441604792151594 体育的信息增益：0.63651416829481278

Tags: 机器学习

← 使用meka实现multilabel classifier windows 平台下python 安装scipy →

扫描二维码，分享此文章